数学小组作业：探究圆的方程

用户头像 发布于 2025-10-07 399 次阅读 数学

数学小组作业：探究圆的方程

一、园的标准方程

i) 圆心在原点上（特殊）

观察这个图形，不难发现它是以原点为圆心，半径为 2 的一个圆形。
那么圆上的任意一点满足什么条件呢？
我们知道，任意一点到圆心的距离都是一定的，那就是——半径 $r$。
那么图中圆上的每一个点都满足 $x^2+y^2=2^2$，这就是这个圆的标准方程。

此时不难发现，一个半径为 $r$ 的圆，以圆心为原点建系，可知这个圆的标准方程就是 $x^2+y^2=r^2$。

ii) 圆心不在原点上（一般）

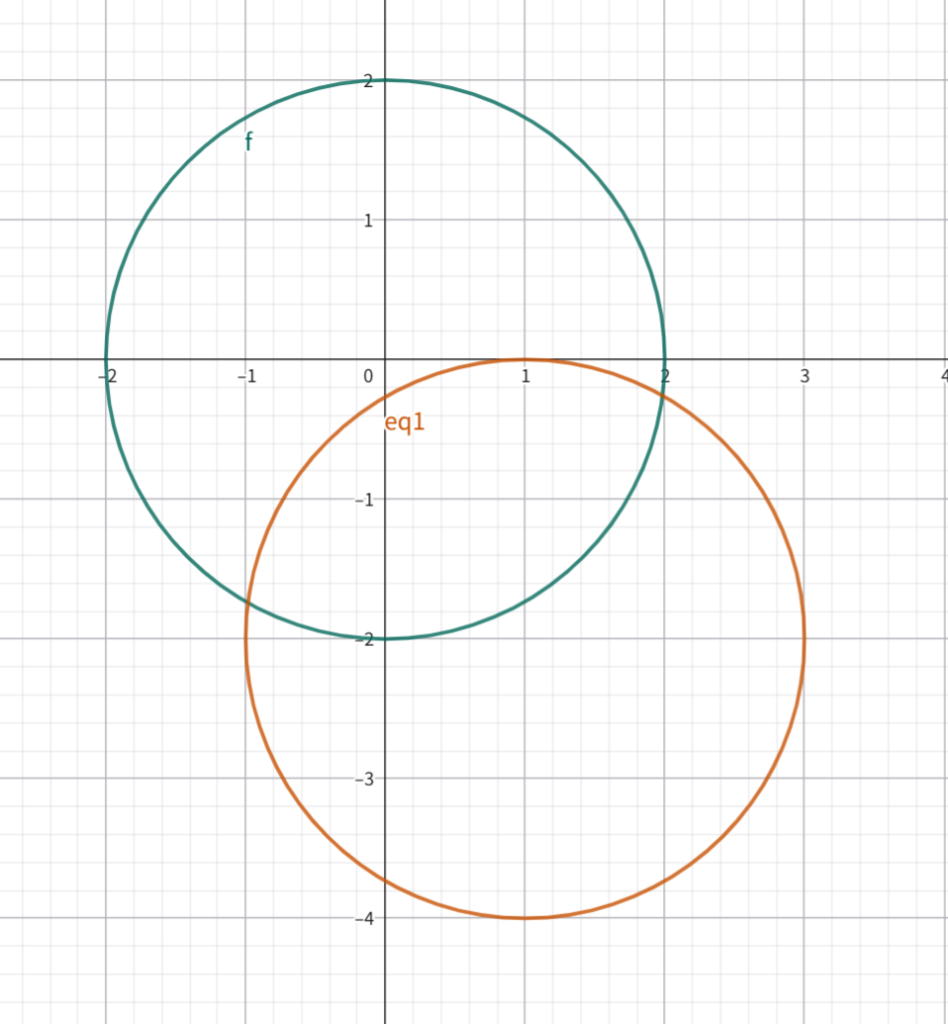
观察上图，多了一个橙色的圆，设以原点为圆心的圆是 $\odot 1$，另一个圆为 $\odot 2$，不难发现 $\odot 2$ 由 $\odot 1$ 向下平移两个单位长度，向右平移一个单位长度得到，那么两个圆的方程有什么联系吗？

  1. 从平移的角度：
    在学习二次函数的顶点式时，我们知道：左加右减，也就是向负半轴方向平移时要加，而向正半轴平移时要减。
    $\because \odot 1 : x^2+y^2=2^2$
    $\therefore \odot 2 : (x-1)^2+(y+2)^2=2^2$
  2. 从两点坐标公式的角度：
    圆上的任意一点 $P(x,y)$ 到圆心 $Q(1,-2)$ 的距离都为 $r$，
    所以根据平面直角坐标系两点之间的距离公式可以得出：
    $\odot 2 : (x-1)^2+(y+2)^2=2^2$

根据上述探究，如果我们知道在平面直角坐标系中有一个圆的圆心坐标为 $(a,b)$，半径为 $r$，那么它的标准方程就是 $(x-a)^2+(y-b)^2=r^2$。

iii) 演示

圆 $(x-a)^2+(y-b)^2=r^2$ 随三个参数改变而改变。

二、特殊的圆——单位圆

i) 定义

单位圆是平面直角坐标系上，圆心为原点，半径为单位长度的圆。

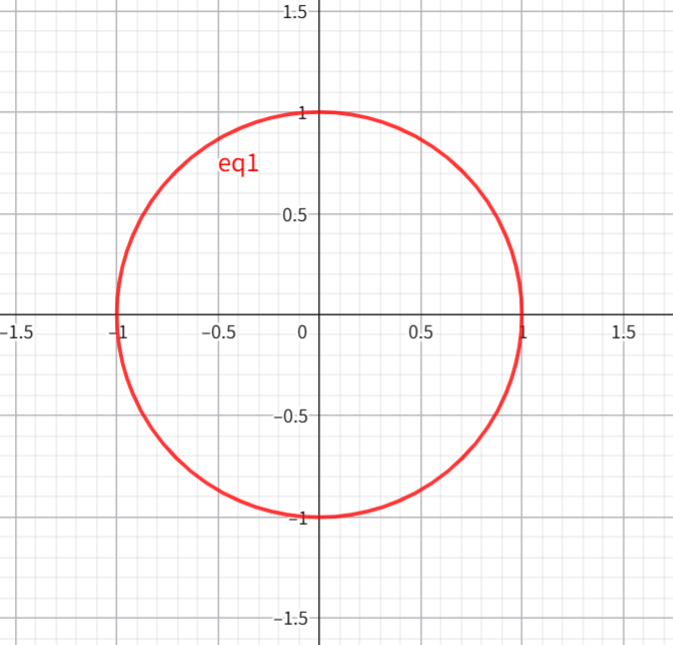
ii) 作用

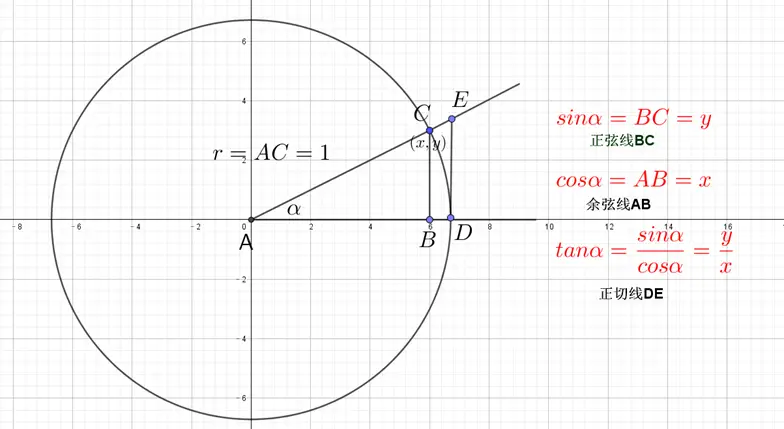
1. 在单位圆上定义三角函数

现在我们有一个角 $θ$，它的顶点在原点，始边在 $x$ 轴正半轴上。

  • 角 $θ$ 的终边与单位圆相交于一个点 $P$。
  • 点 $P$ 的坐标是 $(x, y)$。

那么，角 θ 的三个基本三角函数就定义为：

  • 正弦 $\sin θ$ = $y$（点的纵坐标）
  • 余弦 $\cos θ$ = $x$（点的横坐标）
  • 正切 $\tan θ$ = $y/x$（点的纵坐标与横坐标的比值）

2. 单位圆带来的巨大好处

这种几何定义方式，让许多三角函数的性质变得一目了然：

  1. 直观理解符号变化
    • 在第一象限，$x$ 和 $y$ 都为正，所以 $\sin θ$ 和 $\cos θ$ 都为正。
    • 在第二象限，$x$ 为负，$y$ 为正，所以 $\cosθ$ 为负，$\sinθ$ 为正。
    • 以此类推，这就是著名的”全正切余“口诀的来源。
  2. 理解周期性
    • 当角 $θ$ 增加或减少 $2π$ 时，终边又回到了完全相同的位置，点 $P$ 的坐标 $(x, y)$ 也完全相同。
    • 所以 $\sin (θ + 2π) = \sin θ，\cos(θ + 2π) = \cos θ$。周期性在单位圆上就是“转了一圈回到原点”。
  3. 理解基本恒等式
    • 因为点 $P(x, y)$ 在圆 $x^2+ y^2= 1$ 上，所以直接可得最重要的恒等式：
      $\sin ^2 θ + \cos ^2 θ = 1$
  4. 定义任意大小的角
    • 传统的直角三角形定义只能描述锐角。
    • 单位圆定义可以将三角函数推广到任意角度，无论是正角、负角，还是大于 360° 的角。
  5. 统一理解所有三角函数
    • 正切 (tan θ) 也可以被几何地表示为单位圆上一条切线的长度（这就是“正切”这个名字的由来）。
    • 其他三个三角函数（正割sec、余割csc、余切cot）也都可以在单位圆上找到对应的几何线段表示。

iii) 演示

三、用代码画一个圆

以下是 python 代码实现，可以访问python代码画圆进行体验。
原理：多边形逼近法，其中参数“精度”即正多边形的边数。

import turtle
import math

def draw_circle():
    # 输入参数
    x0, y0 = float(input("圆心x: ")), float(input("圆心y: "))
    r = float(input("半径: "))
    n = int(input("精度: "))
    
    t = turtle.Turtle()
    t.speed(0)
    
    # 直接绘制完整圆
    t.penup()
    t.goto(x0 + r, y0)  # 从最右侧开始
    t.pendown()
    
    # 绘制圆
    for i in range(n + 1):
        a = 2 * math.pi * i / n
        x = x0 + r * math.cos(a)
        y = y0 + r * math.sin(a)
        t.goto(x, y)
    
    # 标记圆心
    t.penup()
    t.goto(x0, y0)
    t.dot(6, "red")
    
    t.hideturtle()
    turtle.done()

draw_circle()