数学3(欧拉函数)
P13880 [蓝桥杯 2023 省 Java A] 互质数的个数
看完题面后很容易想到欧拉函数,
但是 $a^b$ 是一个很大的数,
考虑一些特殊的性质:$\varphi (p^n)=(p-1)p^{n-1}$,($p$ 为质数)
所以令 $a=\prod ^n _{i=1} p_i^{\alpha _i}$,
所以 $a^b=\prod ^n _{i=1} p_i^{b\alpha _i}$
因为欧拉函数是积性函数,
所以 $\varphi (a^b)=\prod ^n _{i=1} \varphi(p_i^{b\alpha _i})=\prod ^n _{i=1} (p_i-1)p_i^{b\alpha _i-1}$
代码:
#include<bits/stdc++.h>
using namespace std;
#define int unsigned long long
const int mod=998244353;
int a,b,ans=1;
int mi(int x,int y){
int ans=1;
while(y){
if(y%2) ans*=x,ans%=mod;
y/=2,x=x*x%mod;
}
return ans;
}
signed main(){
cin>>a>>b;
int x=a;
for(int i=2;i*i<=a;i++){
int p=i,arf=0;
while(x%i==0) x/=i,arf++;
if(arf) ans=(ans*(p-1)%mod*mi(p,arf*b-1))%mod;
}
if(x>1) ans=(ans*(x-1)%mod*mi(x,b-1)%mod)%mod;
cout<<ans%mod;
return 0;
}P2568 GCD
$$
\begin{align}
&\sum_{p\in prime}^n \sum_{i=1}^n \sum_{j=1}^n [(i,j)=p] \\
=&\sum_{p\in prime}^n \sum_{i=1}^{⌊n/p⌋} \sum_{j=1}^{⌊n/p⌋} [(i,j)=1] \\
=&\sum_{p\in prime}^n (2\sum_{i=1}^{⌊n/p⌋} \varphi (i) -1) ^{^*(1)}
\end{align}
$$
预处理欧拉函数的前缀和即可。
$^*(1)$:由于 $(i,j)$ 与 $(j,i)$ 是等价的,所以只需要计算 $i$ 的因子,并把统计结果乘二即可。但是当且仅当 $i=j=p$ 会重复计算,所以减去一个一即可。
代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e7+5;
int n,idx,ans;
int vis[N],prm[N],phi[N];
void euler(){
phi[1]=1;
for(int i=2;i<=n;i++){
if(!vis[i]){
prm[++idx]=i;
phi[i]=i-1;
}
for(int j=1;1ll*i*prm[j]<=n;j++){
vis[i*prm[j]]=1;
if(i%prm[j]==0){
phi[i*prm[j]]=phi[i]*prm[j];
break;
}
else phi[i*prm[j]]=phi[i]*(prm[j]-1);
}
}
}
signed main(){
cin>>n;
euler();
for(int i=1;i<=n;i++) phi[i]+=phi[i-1];
for(int i=1;i<=idx;i++) ans+=phi[n/prm[i]]*2-1;
cout<<ans;
return 0;
}P4388 付公主的矩形
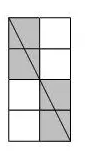
如上图,我们把 $n$ 拆成了 $2*2$,也就是两个日字形,而对于每个日字形,满足周长的一半等于 $2+1$。
这样说可能比较抽象,我们再举一个例子:
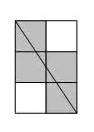
如上图,我们把 $n$ 拆成了 $1*4$,而对于整个矩形,满足周长的一半等于 $4+1$。
也就是说,我们需要首先分解 $n$ 的因数,之后根据因数找到大矩形,且满足矩形周长的一半等于因数加一,但是这个显然只是一个特征,并不能用来得出答案。
但是当我们仔细分析以上两张图的区别,为什么第一张图的对角线会经过一个点?
原因在于大矩形的两边不互质,所以导致有一个等比缩小的矩形与其对角线斜率一致。
所以我们在分解完因数后,枚举小矩形边长,判断是否互质即可。
代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,ans;
int gcd(int a,int b){
if(b==0) return a;
return gcd(b,a%b);
}
signed main(){
cin>>n;
for(int i=1;i*i<=n;i++){
if(n%i!=0) continue;
int x=i+1,y=n/i+1;
for(int j=1;2*j<=x;j++){
int a=j,b=x-j;
if(gcd(a,b)==1) ans++;
}
if(x!=y) for(int j=1;2*j<=y;j++){
int a=j,b=y-j;
if(gcd(a,b)==1) ans++;
}
}
cout<<ans;
return 0;
}P5091 【模板】扩展欧拉定理
欧拉定理:
当 $a,m\in Z$,且 $gcd(a,m)=1$ 时有:
$a^{φ(m)}\equiv 1 \ (mod \ m)$。
所以 $a^{b}\equiv a^{bmodφ(m)} \ (mod \ m)$。
扩展欧拉定理:
当 $a,m\in Z$ 时有:
$$
ab \equiv \begin{cases}
a^b &b<φ(m)\\
a^{b \ mod \ φ(m)+φ(m)} &b≥φ(m)
\end{cases}
(mod \ m)
$$
则有代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int a,m,p;
int phi(int n){
int r=n;
for(int i=2;i*i<=n;i++){
if(n%i==0){
r=r/i*(i-1);
while(n%i==0) n/=i;
}
}
if(n>1) r=r/n*(n-1);
return r;
}
int qp(int x,int y,int mod){
int r=1;
while(y){
if(y&1) r=r*x%mod;
x=x*x%mod;
y>>=1;
}
return r;
}
signed main(){
cin>>a>>m;
p=phi(m);
string s;
cin>>s;
bool f=0;
int b=0;
for(int i=0;i<s.size();i++){
char c=s[i];
b=b*10+(c-'0');
if(b>=p){
f=1;
b%=p;
}
}
if(f) cout<<qp(a,b+p,m);
else cout<<qp(a,b,m);
return 0;
}








Comments NOTHING